With the right tools (the table with all of the number combinations and
elimination sequences on it for example), Kakuro is fairly easy to do. However, there are a number
of curious properties that this number game has.
Sequence Peaks: If you look at the full number sequence sheet (right), you will notice that in the list
of sequences, the number of sequences for each length/sum forms a peak. These peaks increase with
amplitude until they get the the 4 and 5 length sums and then tail off again. The peak height at
the 8 length peaks is, in the middle, the same number of sequences as the peak height in the 2
length peak - ie, four high. If you added in the numbers for a length of 1 and 0, the pattern would be
symmetrical. If any of you have played around with an oscilloscope and a couple of signal generators,
you will see that the peaks like this look like the interference pattern of two frequencies.
Another way of looking at the peaks is like this (B = 11 and C = 12)...
| | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1
0 |
1
1 | 1
2 | 1
3 | 1
4 | 1
5 | 1
6 | 1
7 | 1
8 | 1
9 | 2
0 |
2
1 | 2
2 | 2
3 | 2
4 | 2
5 | 2
6 | 2
7 | 2
8 | 2
9 | 3
0 |
3
1 | 3
2 | 3
3 | 3
4 | 3
5 | 3
6 | 3
7 | 3
8 | 3
9 | 4
0 |
4
1 | 4
2 | 4
3 | 4
4 | 4
5 |
| 2 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
4 | 3 | 3 | 2 | 2 | 1 | 1 | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | |
| 3 | | | | 1 | 1 | 2 | 3 | 4 |
5 | 7 | 7 | 8 | 8 | 8 | 7 | 7 | 5 | 4 |
3 | 2 | 1 | 1 | | | | | | |
| | | | | | | | | |
| | | | |
| 4 | | | | | | | | 1 |
1 | 2 | 3 | 5 | 6 | 8 | 9 | B | B | C |
B | B | 9 | 8 | 6 | 5 | 3 | 2 | 1 | 1 |
| | | | | | | | | |
| | | | |
| 5 | | | | | | | | |
| | | | 1 | 1 | 2 | 3 | 5 | 6 |
8 | 9 | B | B | C | B | B | 9 | 8 | 6 |
5 | 3 | 2 | 1 | 1 | | | | | |
| | | | |
| 6 | | | | | | | | |
| | | | | | | | | |
1 | 1 | 2 | 3 | 4 | 5 | 7 | 7 | 8 | 8 |
8 | 7 | 7 | 5 | 4 | 3 | 2 | 1 | 1 | |
| | | | |
| 7 | | | | | | | | |
| | | | | | | | | |
| | | | | | | 1 | 1 | 2 |
2 | 3 | 3 | 4 | 4 | 4 | 3 | 3 | 2 | 2 |
1 | 1 | | | |
| 8 | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | 1 | 1 | 1 | 1 | 1 |
1 | 1 | 1 | 1 | |
| 9 | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | 1 |
Number of Sequences: For Kakuro,
there are 502 valid sequences. If you are wondering why there are 502 and not 512 (29
which is what you would expect), the valid Kakuro sequences must be at least 2 numbers long. If
you add in the single numbers (1..9) and and introduce a case where there is no number, you get
the total of 512 sequences. Now tell me why it should be 512.
The answer is really in the previous paragraph if you know where to look. If you imagine
each of the nine numbers occupying a place, then each number is either there or not. This is just like
binary - where a digit is either on or off. In this case, we have nine digits so 29 is 512 and
that is how many combinations there are.
If we had 12 fingers (including thumbs) on our hands and had
ended up counting in base 12 instead of base 10, we would have symbols for 10 and 11 (in hexadecimal, we use
A for 10 and B for 11) and we would know how to add up. In that case, Kakuro would have the numbers 1 to B
and there would be 211 or 2048 combinations minus the zero case and the eleven single number cases,
leaving a mere 2036 combinations to choose from. Unfortunately, we can't expect the general public to be
sufficiently fluent in addition in base 12 using A and B for Kakuro to go the same way that Sudoku has gone in
some cases as the value of the symbols used in the Kakuro puzzle has a meaning. Has anybody come across the Sudoku
book called 'Shiteduko'? It reaslises that in Sudoku, you can use any symbols so a nine letter word where
all of the letters are different will do (hence 'shiteduko'). Any word will do so 'computers' or mendacity'
will also work - you can decide for yourself which of those two examples is more appropriate.
NP Complete: Creating Kakuro problems
falls into a catagory of computing problems that are grouped together and called 'NP Complete'. Anybody
that knows a little bit about computer security will have heard of NP complete in connection with
Public Key Cryptography and the use of the term (NPC) usually leads to the inference that the
cryptographic system cannot be broken into. However, it is not as clear-cut as that.
'NP Complete' merely relates to how long it would take to work out the solution
to a problem when the problem can be defined in terms of a number. For example, if a given problem
had a length of 1 and took 1 second to work out, then, if you made the problem have a length of 2
and it took 4 seconds to work out, for 3, 9 seconds and so on, you could say that for a length 'n',
it took n2 seconds to solve. In this case, the power that 'n' is taken to is '2' but it
could be any number - this is called polynomial time and it is where the 'P' in NP comes from.
NP Complete problems don't conform to polynomial time on a deterministic machine. However, this does not mean
that you cannot find a solution. With Public Key Cryptography, you have a large number and you have
to find the only two numbers that will divide into it. Just to make it hard, they are prime numbers.
If you were given 15, you wouldn't take long to work out that it was 3 x 5 multipled together. For
221, you might take longer and even start to think about writing a computer program to work it out
but you would soon come to the conclusion that it was 13 x 17. For numbers that are hundreds or
even thousands of digits long, you need a long time to break it and it doesn't work in polynomial
time - the only way of breaking it is to try out every number until you come across the right one.
Kakuro problems are the same.
The small Kakuro problems you see 8 x 8 can be created in only a few
seconds. The larger problems that are around the 10 x 14 range can take between half an hour and
an hour to create. A 15 x 25 Kakuro would be off the scale. Note that it only takes (literally) a
second to create the mask and another second to fill it in and solve it but with brute force, it
is down to luck as to whether you get that one first or not. As I have tuned the brute force attack on the problem, I have made it all more
efficient - several orders of magnitude more efficient. However, it is far from as good as I
would like it to be. NP Complete doesn't mean that it is not possible to solve the problem with a
computer at any size of the problem, it means that there is in effect an upper limit to the size of
the problem that you can solve that is reasonably practicable. This leads onto an interesting problem...
Puzzle Creation and Limited
Time:
In the
summer of 2007, Implicit
Software Solutions contacted me about producing Kakuro problems for Windows Mobile. The result
is iSS Kakuro with over a million puzzles to do, different sizes and graded in terms of difficulty.
As you know from this page, the problem is NP complete so it produce an interesting problem regarding
the user having a new puzzle within a certain time. It doesn't matter how you design the mask, you
cannot guarantee that any particular attempt to produce a new puzzle will have one in a particular
time - say within 3 seconds. The only solution to this is to have a program that produces genuine
puzzles that are then stored. To run a batch process that produces over a million puzzles on an NP
complete problem requires some limits to be put in place so I used time and the number of attempts
when I ran a modified version of my Perl program.
Also, the problems are graded. This was fairly easy because I knew from the problem
checker just how many times any particular algorithm was used to solve a particular puzzle so these
were graded and divided into appropriate groups of hardness.
One intersting observation was that the process necessarily uses a random seed for
each puzzle. This leads to a situation where a given mask will only have a certain number of valid
puzzles that can be produced using it. For a small puzzle mask, it is easy to see that if you are
producing hundreds, you will probably get duplicates therefore one of the processes that I ran was
to sort them - this includes rotations and reflections - and eliminate all dulicates. In the larger
puzzles, there were no duplicates. As has been observed elsewhere, (see The Scale of
the Problem below), the complexity of the problem rises disproportionately with the size of the
puzzle.
So, with a shameless plug (they did pay me for the work and they have done a good
job of presenting it), if you have a machine that runs 'Windows Mobile', can't keep away from my
Kakuro puzzles but don't have an internet connection everywhere you go, you can get them from
iSS.
Calculations and Brute-Force: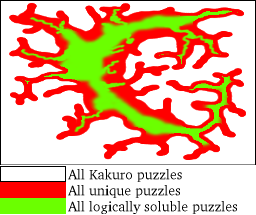
To generate
problems that are unique, you need to have a solver that will produce the only solution for a given Kakuro.
You can see the methods that I use in the tutorial (there wouldn't be much point
in the tutorial if I used any other method and then didn't tell you about it).
On the right, you can see a diagram that represents all Kakuro puzzles with multiple
solutions and as a subset within it, the puzzles that are unique. As a subset of unique puzzles, we have those
that are soluble by the use of logic and maths. To make the red and green areas the same, we would need
methods that currently don't exist (as far as I know) so the only way of solving the ones that
are within the red border but not within the green is to use Brute-Force. On this site, you'll find only the
ones in the green.
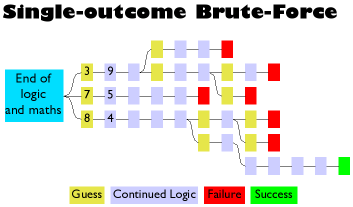However, there is one other method that you can use and that is called 'Brute-Force'.
Brute force is essentially trying out every combination. Say you had a cell (one of an as-yet unsolved
12 in 2) that could have a 3, 7 and 8 in it. You would try it with the 3 (effectively a guess - a low
intelligence method) which would make the next one a 9 and so on; and see if the puzzle worked out.
If you were solving a puzzle that you knew only had one solution, you would leave it at that once you
had a solution. However, if you were using the solver to find a unique solution in an unknown puzzle
(one you were making as opposed to solving), you would work your way back through every arbitrary
decision you had made, trying out all of the other options where you had effectively guessed
until you either worked your way back to the first cell and tried the next number (a 7) and so on, or
found that there was a second solution, in which case, you would know it was not a unique puzzle and
would start to look for the next one. The image above-right represents a Kakuro puzzle with a single solution
and the need to use Brute-Force.
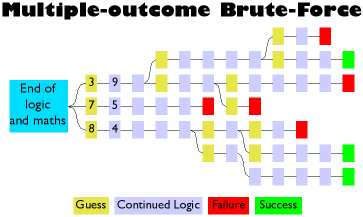If effect, you needn't write any proper algorithms at all (like the ones that produce the
methods you can see in my tutorial) when you use brute force because it would be a waste of time. The program
would produce unique puzzles all of the time. However, there would be no guarantee that they could be solved
using just logic and maths. In effect, using Brute-Force is just lazy programming and when the person
attempting to solve the puzzle finds that they cannot do it unless they spend hours trying out every
combination of numbers, they will be put off by the experience.The image above-right represents a
different Kakuro puzzle, this time with several solutions and the need to use Brute-Force.
The Scale of the Problem:
Kakuro masks are filled with numbers in order to get the sums that you see in the problem - your only clues.
However, have you wondered just how they are put there? You could just put any old numbers in there (as long
as they were from 1 to 9 inclusive and didn't repeat) and try that but the chances of getting a combination
that only produced a single solution (or any solution) is pretty low. You notice that in all of those
Kakuro books, they supply you with a list of unique numbers? Well, if you use only the unique number
sequence, you end up with a situation where you cannot always get a unique number in there so you use
any number.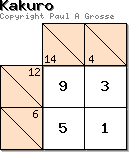 
That also produces a very low success rate. The answer is to use two sums such that where
they intersect, there is only one number that can exist there. On the number lists on this site, you
can see an excluded number list and if you look at the tutorial, you can see how to use it. So, just
how many combinations of puzzles are there?
The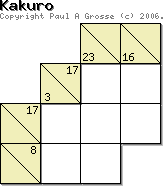
puzzle on the left is an example of how small it can get. There are 12 combinations
of sums that will leave only one intersecting value. In the example, you can see that for 12 in 2, the
excluded values are '12...6...'. For a 4 in 2, the excluded values are '.2.456789'. If we 'OR' these
lists of numbers (that is to say that if a number is found in one 'or' the other, it ends up in our
final list), we end up with '12.456789' so the only value not excluded is 3 which goes where those
two sums intersect. The other values in the intersecting pair are necessarily the number bonds of these,
ie, 9 and 1 but the number that goes in the fourth cell can be anything other than the numbers in the
two sums already, ie, 9 or 1. So, in this other cell, we could have one of '.2345678.'. In other words,
for every one of the 12 elimination combinations, we can have seven variants or,
7 x 12 = 84 combinations in a 2 x 2 Kakuro puzzle and that is excluding
mirror images and rotations.
So, how many combinations are there for a 3 x 3 Kakuro? What, if
you enforce the rule that it has to be rotationally symmetrical, happens when you add a variant that
has opposite corners removed? In a 4 x 4, you can remove more of a corner or have all four
corners removed. In a 5 x 5, you can take out the centre cell as well. Very quickly, our 84
solution problem has become a mess of complexity in much the same way that Schodinger's Wave Equation is
good for Hydrogen but is not particularly good for cellulose
Brute Force: Brute force sounds vicious
and, well, brutal but it is just the act of trying out every combination without knowing how to produce
a perfect result first time. If we go back to our problem of finding the two prime numbers that make up
221, the only way is to try out every combination. In short, such a program would loop through a test
that takes the current value (start at 2) and goes all of the way up to one short of the number itself
(220), looking for a whole number that is produced when you try to divide 221 by the current number.
With Kakuro problems, it is the same.
But surely, there is a way of making the search quicker? Well, there is. We know that we
are looking for one number multiplied by another so that the product is no larger than 221 so we can
start off by limiting the search range from 2 to the square root of the target number (so the square
root of 221 is 14.8660687473185 so we know that there is no point in going higher than 15 (or even 14).
But that is not all. We also know that 2 is the only even prime number so we can look to see if it is
even (ie, does 2 divide exactly into 221) and then look only at the odd numbers up to 15. It is similar
with Kakuro.
The object of the program is to output a file that is a png image of a valid Kakuro
puzzle. If we were to use 'true brute force', we would open a file and then just print random bits to
it. However, this is not the most efficient way of doing things and there are plenty of ways to make the
search better.
| Program |
Solve problem |
Verify solution |
Human
involvement (verifying) |
Problems |
Pure brute force:
open a file and print random numbers to it. |
Very quick but almost all output isn't even a valid PNG file. |
User cannot open files even to have a look. |
~100 per cent. |
Chance of producing even a valid PNG is incredibly low. |
| Use an image library in the program but print random dots to it. |
Very quick but almost all output just resembles white noise on a TV. |
User spends most of time opening files that are nonsense. |
~100 per cent |
Chance of producing anything that resembles a number is extremely low. |
Create an array and fill with random numbers (zero signifying a non-cell).
graphical output reflects this. |
Takes a second or so to create mask. |
Almost all Kakuro-looking puzzles are insoluble or have multiple solutions. |
still ~100 percent. |
Easy to produce a kakuro-like puzzle but almost all are not valid. |
| Create a 'solver' routine that only allows viable (unique, soluble) puzzles as output |
Takes hours for a very small puzzle (5x5). |
Computer now does this in less than a second. |
None. All done by the program |
Takes a very long time to produce something that works |
| Use unique sets where they will fit. |
Still takes a very long time to create a small puzzle. |
< 1 second. |
None. |
Still takes a long time. |
| Whereever possible, use an eliminating set or a unique set. |
Speeds things up considerably. Now, we are taking a few tens of seconds for an 11x11 puzzle. |
< 1 second. |
None. |
Still takes a long time for large puzzles. |
| ? |
? |
? |
? |
? |
| ? |
Right first time... |
< 1 second. |
None. |
None. |
Copyright (c) 2006 Paul Grosse. All rights reserved.
