If the second stage of a
two stage rocket provides no additional
thrust, it is called a dart.
By ending the rocket
description with the word "DART",
the computer model ignores the capacity of
the rocket, the amount of water, the
pressure, the air impulse, nozzle diameter
and so on. Instead, it uses the rocket
diameter, coefficient of drag, initial speed
and angle to calculate its trajectory.
Optimising
a Dart
A
significant difference between the dart
optimisation and the normal second stage
optimisation is that the dart simply rests
upon the mechanism. Once the booster starts
to slow down, separation occurs. Therefore,
the pressure in the booster has no influence
on the time of separation.
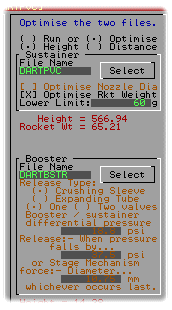In the two stage optimisation
with a dart, the sustainer and the booster
files are prepared and loaded as normal but
when the sustainer file is loaded, the
program recognises that it is dealing with a
dart so the nozzle diameter optimisation for
the sustainer and the release mechanism for
the booster are both disabled as in the
screen shot on the left.
As with normal two stage optimisation, it
is still possible to optimise for maximum
height or maximum distance, or simply to run
the sustainer and booster files without
optimisation. Running the two files can be
used to find out how much effect changing the
amount of water or one of the other variables
has on performance.
One parameter that is left to optimise on
the sustainer is its weight. Normally, in a
two stage optimisation, if the sustainer
provides very little impulse, the
optimisation runs away, being divergent. In
order to combat this, the optimisation for a
dart runs by optimising the booster for the
weight of the dart and then calculates the
height (or distance) the dart travels. Then
it increases or decreases the weight of the
dart according to a similar strategy that
provides the optimisation for the amount of
water in the booster. The weight is increased
by large amounts until no gain in height (or
distance) is found and then it is decreased.
Once the optimum height (or distance) is
found for large changes, the process is
repeated for smaller changes, and then
smaller changes still, until an optimum value
is found.
Return to 2
Stage Optimisation
Copyright
©2000 Paul Grosse. All Rights Reserved